Artykuł wyjaśnia słynną zagadkę logiczną o kapeluszach, często wykorzystywaną w rekrutacji do Google, przedstawiając jej zasady i krok po kroku tłumacząc zwycięską strategię, która pozwala uratować większość uczestników.
Strategia parzystości ratuje 99% więźniów poznaj rozwiązanie zagadki o kapeluszach z Google
- Zagadka o kapeluszach to klasyczny problem logiczny, popularny w rekrutacji do firm technologicznych, takich jak Google.
- W podstawowej wersji 100 więźniów w kolejce, z kapeluszami w dwóch kolorach, widzi tylko osoby przed sobą i musi odgadnąć kolor swojego kapelusza.
- Kluczem jest ustalenie strategii przed rozpoczęciem, gdzie ostatnia osoba w kolejce przekazuje kluczową informację.
- Najskuteczniejsza strategia opiera się na systemie parzystości (np. liczeniu czerwonych kapeluszy) i pozwala na uratowanie 99 ze 100 osób.
- Pierwszy okrzyk (osoby na końcu) koduje informację o parzystości, a kolejne osoby dedukują swój kolor na podstawie tej informacji i własnych obserwacji.
- Istnieją warianty zagadki, np. z mniejszą liczbą osób, większą liczbą kolorów (wymagające arytmetyki modularnej) lub innym ustawieniem.
Poznaj problem, który testuje umysły najlepszych kandydatów
Zagadka o kapeluszach to klasyczne wyzwanie logiczne, które stało się sławne dzięki wykorzystywaniu jej w procesach rekrutacyjnych w firmach technologicznych, takich jak Google. Jej celem jest ocena zdolności analitycznego myślenia i kreatywności w rozwiązywaniu problemów. To nie jest zwykła łamigłówka; to test, który potrafi wyłonić kandydatów o wyjątkowym sposobie myślenia.
Dlaczego ta łamigłówka stała się legendą w świecie IT?
To, co czyni tę łamigłówkę legendą w branży IT, to nie tylko samo rozwiązanie, ale proces dochodzenia do niego. Pokazuje ona, jak ważne są myślenie systemowe, zdolność do współpracy (nawet w sytuacji zagrożenia życia) i dedukcja umiejętności kluczowe w codziennej pracy programistów i inżynierów. Zrozumienie tej zagadki to dowód na to, że potrafisz analizować złożone problemy i znajdować eleganckie rozwiązania.
Zasady gry o najwyższą stawkę: 100 więźniów i dwa kolory kapeluszy
Jak wygląda ustawienie? Kto kogo widzi?
Wyobraźmy sobie 100 więźniów ustawionych w jednej, długiej linii, jeden za drugim. Każdy z nich ma na głowie losowo nałożony kapelusz może być czerwony lub niebieski. Kluczowe jest to, że każdy więzień widzi kapelusze wszystkich osób stojących przed nim, ale nie widzi swojego własnego ani kapeluszy osób za nim. To tworzy specyficzną hierarchię obserwacji.
Cel: Ocalić jak najwięcej osób. Ale jak to zrobić?
Celem jest uratowanie jak największej liczby więźniów. Każdy musi wykrzyczeć kolor swojego kapelusza. Błędna odpowiedź oznacza wyrok śmierci. Napięcie rośnie z każdym kolejnym więźniem. Na szczęście, więźniowie mają możliwość ustalenia strategii przed rozpoczęciem tej śmiertelnie niebezpiecznej gry. To właśnie ta możliwość strategicznego planowania jest sednem zagadki.
Kluczowe ograniczenie: Możesz wypowiedzieć tylko jedno słowo
Komunikacja jest ściśle ograniczona. Każdy więzień może wypowiedzieć tylko jedno słowo kolor swojego kapelusza. Kolejność wypowiedzi jest również z góry ustalona: zaczyna ostatnia osoba w kolejce, a kończy pierwsza. To właśnie te ograniczenia sprawiają, że znalezienie skutecznej strategii jest tak fascynujące.
Strategia, która ratuje 99% skazanych: wyjaśniamy krok po kroku
Bohater na końcu kolejki: Dlaczego jego rola jest najważniejsza?
Osoba stojąca na samym końcu kolejki, oznaczmy ją numerem 100, ma unikalną pozycję. Widzi ona wszystkie 99 kapeluszy przed sobą. Jej zadanie nie polega na odgadnięciu koloru własnego kapelusza jej szansa na przeżycie wynosi jedynie 50%. Jej prawdziwa rola polega na przekazaniu kluczowej informacji pozostałym więźniom. Poświęca ona swoją pewność przeżycia dla dobra większości.
Magia parzystości: Jak informacja jest kodowana w jednym słowie?
Kluczem do sukcesu jest strategia oparta na parzystości. Więźniowie umawiają się przed rozpoczęciem gry. Osoba numer 100 liczy kapelusze jednego, ustalonego koloru powiedzmy, czerwonego wśród tych 99, które widzi. Jeśli liczba czerwonych kapeluszy jest parzysta, krzyczy "czerwony". Jeśli liczba jest nieparzysta, krzyczy "niebieski". Ważne jest, aby ta konwencja była konsekwentnie przestrzegana. W ten sposób, jedno słowo koduje informację o parzystości, a nie bezpośrednią próbę odgadnięcia własnego koloru.
Efekt domina: Jak drugi więzień odczytuje wiadomość?
Teraz prześledźmy rozumowanie przedostatniego więźnia, numer 99. Słyszy on okrzyk osoby numer 100, który informuje o parzystości czerwonych kapeluszy. Jednocześnie widzi 98 kapeluszy przed sobą. Liczy czerwone kapelusze, które widzi. Porównuje tę liczbę z informacją o parzystości przekazaną przez więźnia numer 100. Jeśli na przykład ostatni więzień krzyknął "czerwony" (parzysta liczba czerwonych), a więzień numer 99 widzi przed sobą nieparzystą liczbę czerwonych kapeluszy, to wie, że jego własny kapelusz musi być czerwony, aby suma była parzysta. W ten sposób, więzień numer 99 jest w stanie ze 100% pewnością wydedukować kolor swojego kapelusza.
Pełna dedukcja: Prześledźmy rozumowanie więźnia numer 98, 97 i kolejnych
- Słuchanie i obserwacja: Każdy kolejny więzień (np. numer 98) słyszy okrzyki wszystkich poprzednich osób, które już odgadły swoje kapelusze, oraz widzi kapelusze osób stojących przed nim.
- Aktualizacja informacji o parzystości: Na podstawie usłyszanych okrzyków i obserwowanych kapeluszy, więzień aktualizuje informację o parzystości liczby czerwonych kapeluszy. Na przykład, jeśli więzień 100 powiedział "czerwony" (parzysta liczba), a więzień 99 powiedział "niebieski" (co oznacza, że odgadł swój czerwony kapelusz), to więzień 98 wie, że łączna liczba czerwonych kapeluszy widzianych przez niego i jego własny kapelusz musi być parzysta.
- Wnioskowanie: Jeśli więzień 98 widzi przed sobą określoną liczbę czerwonych kapeluszy, a wie, jaka powinna być parzystość całości (uwzględniając już odgadnięte kapelusze), może precyzyjnie określić kolor swojego kapelusza.
- Pewne odgadnięcie: Dzięki tej dedukcji, każdy więzień (oprócz ostatniego) jest w stanie bezbłędnie odgadnąć kolor swojego kapelusza.

Co jeśli zmienimy zasady? Popularne warianty zagadki o kapeluszach
Mniej osób, ta sama logika: Czy zagadka z 10 więźniami jest prostsza?
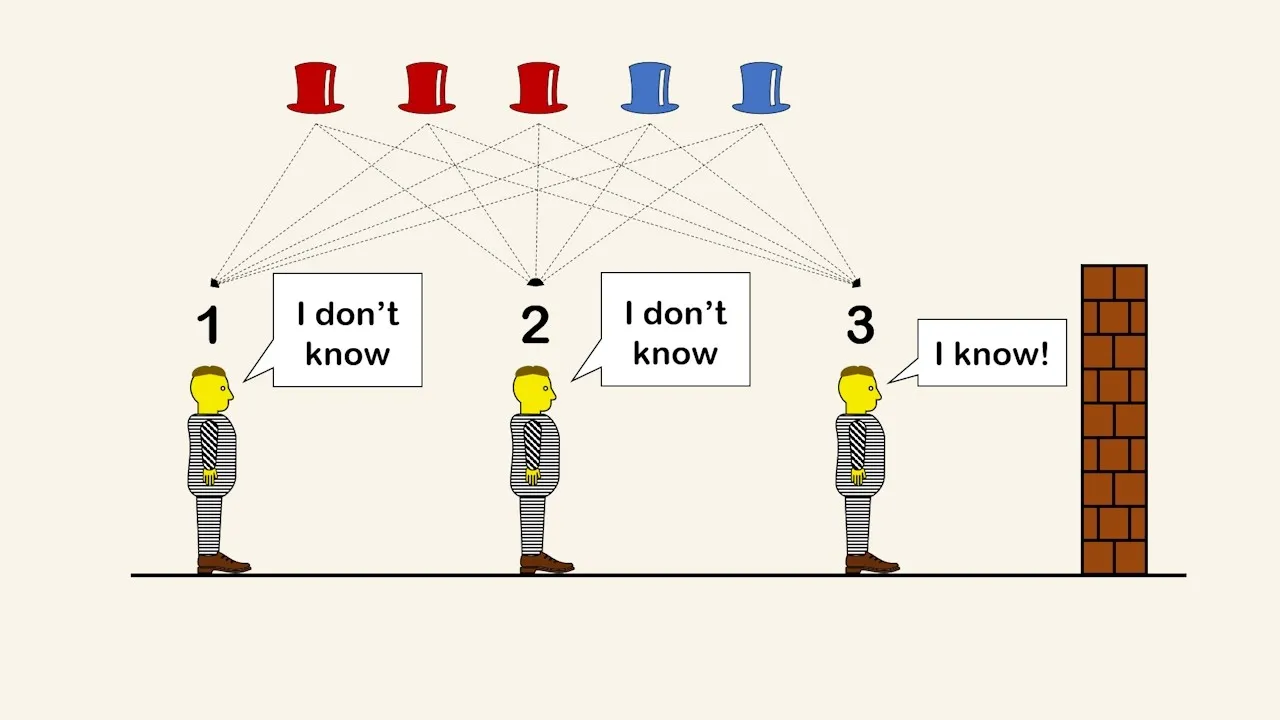
Oczywiście, zagadka ta występuje w wielu wariantach. Wersje z mniejszą liczbą osób, na przykład 10, 4 czy 3 więźniów, są doskonałym sposobem na lepsze zrozumienie mechanizmu. Podstawowa logika i strategia parzystości pozostają te same, ale mniejsza skala problemu pozwala łatwiej prześledzić każdy krok dedukcji i zobaczyć, jak efekt domina działa w praktyce.
Gdy pojawia się trzeci kolor: Jak zmodyfikować zwycięską strategię?
Co jeśli kapelusze mogą być nie tylko czerwone i niebieskie, ale także zielone? Wtedy prosta strategia parzystości przestaje wystarczać. Konieczne staje się zastosowanie arytmetyki modularnej. Każdemu kolorowi przypisuje się wartość liczbową (np. czerwony=0, niebieski=1, zielony=2). Następnie sumuje się wartości kolorów widzianych kapeluszy, a informacja przekazywana przez ostatnią osobę to reszta z dzielenia tej sumy przez liczbę dostępnych kolorów (w tym przypadku 3). Kolejni więźniowie, znając już część sumy i resztę, mogą wydedukować wartość swojego kapelusza.
Trzech mędrców i pięć kapeluszy: Inna zagadka, inne rozwiązanie
Warto wspomnieć o innej, klasycznej zagadce, często mylnie łączonej z problemem kapeluszy: zagadce "trzech mędrców i pięciu kapeluszy". W tej wersji mamy trzech mędrców, którym pokazuje się pięć kapeluszy (trzy czarne i dwa białe). Każdy z nich zakłada jeden kapelusz na głowę, a pozostałe trzy są ukrywane. Mędrcy widzą kapelusze pozostałych dwóch. Celem jest odgadnięcie koloru własnego kapelusza. Tutaj strategia nie polega na bezpośrednim przekazywaniu informacji, lecz na dedukcji z braku odpowiedzi lub analizie zachowania innych. To zupełnie inny rodzaj logicznego wyzwania.
Więcej niż zagadka: czego uczy nas problem kapeluszy?
Myślenie systemowe: Jak współpraca i ustalona strategia prowadzą do sukcesu?
Zagadka o kapeluszach to doskonała lekcja myślenia systemowego. Pokazuje, że indywidualny sukces często zależy od dobrze zaplanowanej współpracy i jasnego podziału ról. Ustalenie strategii przed rozpoczęciem gry, gdzie każdy element systemu (więzień) odgrywa określoną, choć czasem trudną rolę (jak poświęcenie ostatniej osoby), jest kluczem do osiągnięcia wspólnego celu. To pokazuje, jak ważna jest komunikacja i zaufanie w zespole.
Myślenie "out of the box": Dlaczego najbardziej oczywiste rozwiązania zawodzą?
Najbardziej oczywiste rozwiązania, takie jak próba zgadywania koloru kapelusza na chybił trafił, prowadzą do katastrofy. Zagadka wymaga myślenia "poza schematami". Musimy zaakceptować, że jedna osoba może poświęcić swoją pewność przeżycia dla dobra grupy. To uczy nas, że czasami najbardziej efektywne rozwiązania wymagają odejścia od intuicyjnych, indywidualnych strategii na rzecz bardziej złożonych, grupowych podejść.
Jak wykorzystać ten typ logiki do rozwiązywania codziennych problemów?
Logika i strategiczne myślenie, które są testowane przez zagadkę o kapeluszach, mają zaskakująco szerokie zastosowanie. Umiejętność analizowania informacji, dedukcji, planowania i przewidywania konsekwencji swoich działań jest nieoceniona w codziennym życiu. Niezależnie od tego, czy rozwiązujemy problem w pracy, podejmujemy ważną decyzję finansową, czy nawet planujemy rodzinne wakacje, podejście oparte na logicznym wnioskowaniu i strategicznym planowaniu może prowadzić do znacznie lepszych rezultatów.
Przeczytaj również: Skąd się wzięło jabłko? Fascynująca historia i symbole
Kluczowe wnioski i Twoja droga naprzód: Podsumowanie zagadki o kapeluszach
Przeszliśmy przez zawiłości słynnej zagadki o kapeluszach, która od lat stanowi wyzwanie dla umysłów kandydatów do największych firm technologicznych. Mam nadzieję, że teraz rozumiesz, jak strategia oparta na parzystości pozwala uratować 99 ze 100 więźniów, pokazując potęgę logicznego myślenia i ustalonej strategii.
- Sukces w zagadce o kapeluszach zależy od wcześniejszego ustalenia strategii, a nie od indywidualnego zgadywania.
- Kluczem jest przekazanie informacji przez ostatnią osobę w kolejce, która poświęca swoją pewność przeżycia dla dobra grupy.
- Strategia parzystości pozwala na niemal bezbłędne odgadnięcie koloru kapelusza przez pozostałych uczestników.
- Warianty zagadki, np. z większą liczbą kolorów, wymagają bardziej zaawansowanych technik, takich jak arytmetyka modularna.
Z mojego doświadczenia wynika, że ta zagadka doskonale ilustruje, jak ważne jest patrzenie na problem z szerszej perspektywy i wykorzystywanie dostępnych informacji w sposób niestandardowy. Często w życiu zawodowym i prywatnym napotykamy sytuacje, które wydają się beznadziejne, jeśli podchodzimy do nich z pojedynczej perspektywy. Kluczem jest znalezienie wspólnego mianownika i ustalenie jasnych zasad komunikacji, tak jak zrobili to więźniowie. To właśnie ta umiejętność współpracy i strategicznego myślenia odróżnia przeciętne rozwiązania od tych naprawdę genialnych.
A jakie są Twoje przemyślenia na temat tej zagadki? Czy kiedykolwiek spotkałeś się z podobnym problemem logicznym w praktyce? Podziel się swoimi doświadczeniami w komentarzach!

